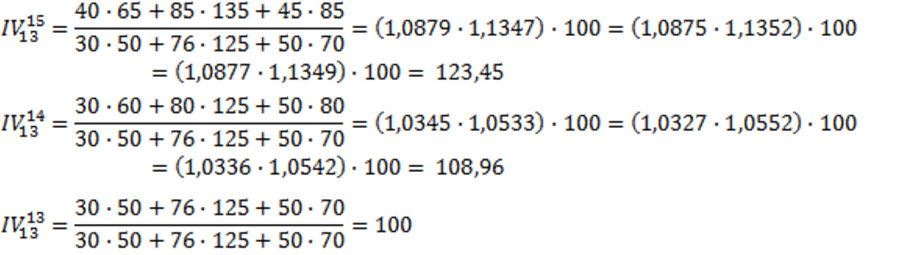Una introducción a los números índice
4. Números índices complejos
4.1. Ejemplo de números índices complejos
En la siguiente tabla, se presentan los datos para una sencilla cesta de consumo compuesta por tres productos: leche, carne y fruta, durante los años 2013, 2014 y 2015.

Se pide:
a) Obtener los índices de precios de Laspeyres, Paasche y Fisher para los tres años, de precio y cantidad, considerando 2013 como año base.
b) Obtener los índices de cantidad y valor (Laspeyres, Paasche y Fisher)
RESPUESTA
Partimos de las formulas conocidas de cada índice de precios (Laspeyres, LP, Paasche, Pp y Fisher, Fp):
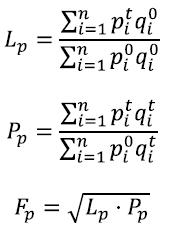
Nótese que el llamado índice ideal de Fisher es la raíz cuadrada de los dos primeros expuestos.
Aplicando las formulas a los datos del problema, proporcionados en el enunciado, nos queda para cada uno de los años, el siguiente valor de los índices:


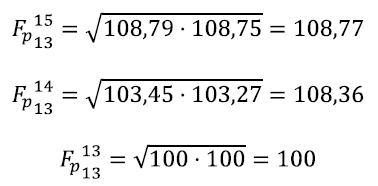
b) Vamos a calcular ahora los índices de cantidad. En este caso vamos a medir la evlolución en el periodo de la cesta de unidades físicas de leche, carne y fruta que integra nuestra cesta.
Partimos de las fórmulas para los mismos tres índices anteriores (Laspeyres, Lq, Paasche, Pq y Fisher, Fq):
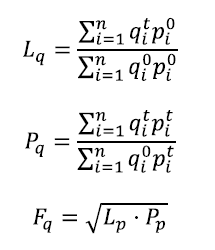
Aplicamos estas formulas a los datos proporcionados por el ejercicio, llegando a los siguientes resultados:


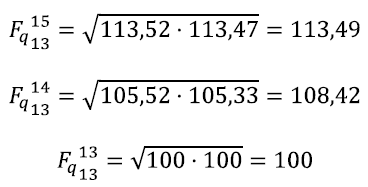
Ahora, calculamos los índices de valor, a partir de su formulación y los datos de la tabla:
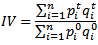
El indice valor tiene la particularidad de ser igual al producto de los índices de Laspeyres y Paasche (siendo uno de precios y otro de cantidad, es decir: Lp·Pq, o, Lq·Pp), o bien el producto de los índices de Fisher de precio y cantidad (Fp·Fq):