Una introducción a los números índice
| Sitio: | Aula Virtual de Formación en línea (ISMIE) |
| Curso: | (C23) El INE.es como herramienta educativa |
| Libro: | Una introducción a los números índice |
| Imprimido por: | Invitado |
| Día: | viernes, 13 de febrero de 2026, 18:14 |
Descripción
El objetivo de este libro es enseñar la teoría de números índices, en sus diversas modalidades, y en particular profundizar en el Índice de Precios al Consumo (IPC).
1. Introducción
Un número índice se define como una medida estadística que compara una magnitud o variable en dos situaciones distintas, una de las cuales se considera base o referencia.
El principal problema que intentan resolver los números índices es conseguir una expresión cuantitativa representativa de un conjunto de agregados elementales heterogéneos que no pueden medirse en unidades físicas comunes. Es decir, el número índice engloba detrás de una sola cifra una gran cantidad de información.
¿Con qué objeto? A través del número índice, generalmente, podremos analizar la evolución en el tiempo de aquello que queramos estudiar. Por ejemplo: en el Indice de Precios al Consumo (I.P.C.) la evolución de los precios.
2. Clasificación de los números índice
Podemos clasificar los números índice siguiendo diversos criterios. En los siguientes puntos de este capítulo veremos tres criterios de clasificación.
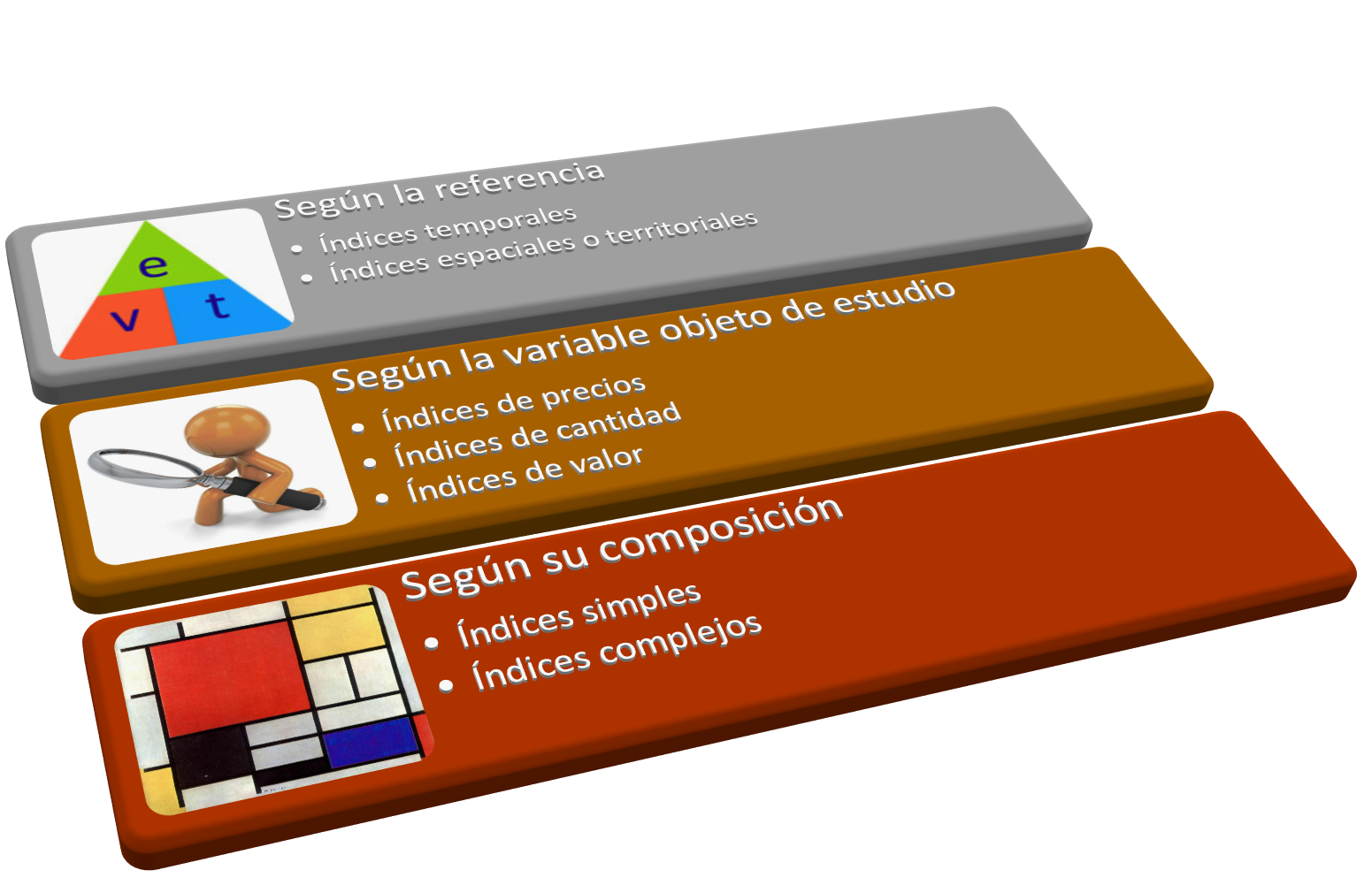
2.1. Según la referencia
Una primera clasificación de los números índices viene determinada por las situaciones que pretende medir. De esta forma, diferenciamos entre:
a) Índices temporales - en la mayoría de los casos los índices se refieren al tiempo, midiendo la variable objeto en dos periodos diferentes de tiempo, con el objeto de dar una medida de su evolución. Sería por ejemplo la razón del valor de una cesta de la compra en dos periodos distintos (diciembre 2015 y diciembre de 2014, por ejemplo).
b) Índices espaciales o territoriales - se utilizan cuando las situaciones que se pretenden comparar son áreas geográficas o territorios. El ejemplo más característico de índices espaciales son las Paridades de Poder Adquisitivo (PPA), que comparan, entre otras variables, los niveles de precios de las capitales de los países de la Unión Europea (UE). Se trata de una estadística cuyo cálculo es responsabilidad de la Oficina de Estadística de la UE (Eurostat), que considera la UE o de la Unión Monetaria (UM) como territorios de referencia; así, países con índices con valores superiores a 100 indican que sus niveles de precios están por encima de la media, y aquellos con índices por debajo de 100 tienen precios inferiores a la media del territorio de referencia.
Para más detalles de este estudio consúltese http://ec.europa.eu/eurostat/web/purchasing-power-parities/overview
2.2. Según la variable objeto de estudio
Podemos clasificar igualmente los números índices atendiendo a la variable objeto de estudio. Según cuál sea esta, diferenciamos entre:
- a) Índices de precios - los más destacados, entre los calculados por el INE, son el Índice de Precios de Consumo (IPC) o el Índice de Precios Industriales (IPRI).
- b) Índice de producción física - el más relevante es el Índice de Producción Industrial (IPI).
- c) Índices de valor - destacan el Índice de Comercio al por Menor (ICM), que establece comparaciones temporales entre el valor de las ventas de este tipo de comercio, el Índice de Cifra de Negocios Empresarial (ICNE), o los Indicadores de Actividad del Sector Servicios (IASS), que miden la evolución de las cifras de negocios de la industria y los servicios, respectivamente. También destacan el Índice de Salarios y el Índice de Ocupación, que utilizan variables de niveles salariales y número de empleados, respectivamente.
Todos ellos se pueden consultar en España en www.ine.es

2.3. Según la composición y forma de construcción
Una tercera clasificación de números índice, es según la composición y forma de construcción que tenga el mismo. Según este criterio, podemos distinguir dos tipos:
a) Índices simples o índices elementales - representan la expresión más básica en el cálculo de los números índices. Relaciona el dato de una variable en dos momentos de tiempo (momento t y momento 0).
b) Índices complejos o agregados - se calculan como agregaciones de índices simples. En su cálculo pueden intervenir diferentes factores de ponderación dependiendo de la naturaleza del índice.
Este es un aspecto esencial de este bloque de contenidos, por lo que analizaremos unos y otros, en mayor profundidad, en los puntos 3 y 4 siguientes.
3. Números índices simples
Representan la expresión más básica en el cálculo de los números índices. De hecho, su principal característica radica en la imposibilidad de desagregar más los componentes utilizados en su cálculo. En algunos manuales estadísticos, los índices simples son considerados como relaciones de variables, sin llegar a ser considerados índices como tal.
Su construcción es como sigue:
Como se puede ver, un índice simple relaciona el dato de una variable en dos momentos de tiempo (momento t y momento 0 o base). Generalmente se multiplican por 100, de tal manera que el valor del índice para el periodo base siempre sea 100 y no 1 (en el periodo base o periodo 0). Así:
Según la variable que estudien, bien si son precios o cantidades o magnitudes valor, se puede hablar de tres tipos fundamentales de índices: índices de precios, índices de cantidad e índices de valor, respectivamente.
Adicionalmente, estos índices pueden estar referenciados respecto a un periodo base (índice en serie) o respecto al periodo inmediatamente anterior (índice en cadena).
Veamos un ejemplo de su construcción y elaboración de series y cadenas a través de un sencillo ejemplo que exponemos en la siguiente tabla. Como puede observarse, hemos extraído de la web del I.N.E. los datos totales, para España y para ambos sexos, de las personas con discapacidad (representado en miles de personas), en el periodo comprendido entre los años 2009 y 2014:
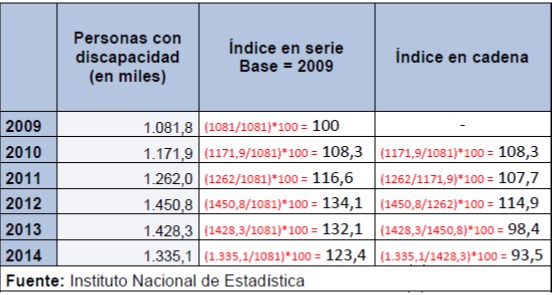
En la segunda y tercera columna, podemos ver (en rojo) cómo hemos calculado cada uno de los números índice simples, a través de una relación entre el dato de la variable en cada año y el dato de la misma variable en el periodo base.
En la segunda columna (índice en serie), el periodo base es fijo y siempre el 2009. En cambio, en la tercera columna (índice en cadena), el periodo base es el año inmediatamente anterior a cada caso.
4. Números índices complejos
Se calculan como agregaciones de índices simples. En su cálculo pueden intervenir diferentes factores de ponderación dependiendo de la naturaleza del índice. Sin embargo, el potencial real de los números índices se pone de manifiesto cuando se trata de medir varias variables o elementos en esas dos situaciones, ya que es en ese momento cuando es preciso corregir el problema que supone la agregación de variables con diferentes unidades de medida (heteromensurabilidad). Un ejemplo de su necesidad, lo vemos cuando pretendemos construir un índice de precios de una cesta de la compra donde se incluyen productos diferentes (comida, bebida, ropa, etc.), o bien, el caso de un índice bursátil compuesto por la cotización de títulos de empresas y sectores diferentes (comunicaciones, químicas, eléctricas, bancos, etc.).
Para construir este tipo de índices, debemos de resolver dos cuestiones principales:
- El promedio - se debe de abordar la cuestión de cómo se van a agregar los índices simples para hallar el valor final del promedio que es todo índice complejo. En este caso, podemos utilizar la media aritmética, geométrica, armónica o agregativa, con el fin de solventar este propósito. Estas medias podrán ser, a su vez como explicamos a continuación, ponderadas o no ponderadas.
- Las ponderaciones - el indice complejo será un valor promedio de los indices que lo componen, por lo que una de las primeras cuestiones es establecer ese peso de los números índice simples dentro del valor del indice complejo final. Si la ponderación de cada índice simple es la misma, hablamos de índices complejos sin ponderar; por el contrario, cuando la ponderación de cada índice simple es distinta, hablamos de índices complejos ponderados.
A partir de aquí, trabajaremos con este tipo de índices. Podremos ver la construcción de los dos más utilizados: el índice de Laspeyres y de Paasche, exponiendo las ventajas e inconvenientes de cada uno.
Siendo:
wi = ponderación del elemento i.
pit = precio del bien i en el momento actual t.
pi0 = precio del bien i en el periodo base 0.
qit = cantidad (consumida, vendida o producida) del bien i en el momento actual t.
pi0 = cantidad del bien i en el periodo base 0.
- Índice de Laspeyres (IL)- es la media aritmética ponderada de los índices simples que lo integran. Como ponderación se utiliza, para cada artículo, el valor de la cantidad (consumida, vendida o producida) del bien iésimo en el período base al precio de ese mismo período base (wi=pi0·qi0).
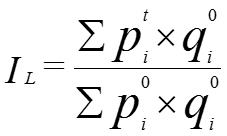
El índice de Laspeyres tiene como principal ventaja el hecho de utilizar cantidades de un solo periodo, el periodo base, por lo que las variaciones que pueda experimentar el índice serán solamente atribuibles a la variación en los precios. Entre las desventajas, destaca el hecho de que este índice pondera más los productos cuyos precios aumentan; igualmente, tampoco refleja los cambios que hayan podido haber en los patrones de compra entre el periodo base y el periodo actual.
- Índice de Paasche (Ip) - es la media aritmética ponderada de los índices simples que lo integran. Como ponderación se utiliza, para cada artículo, el valor de la cantidad (consumida, vendida o producida) del bien íesimo en el periodo actual a precio del período base (wi=pi0·qit).
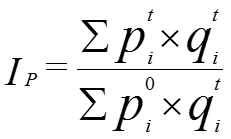
Obsérvese que el índice de Paasche tiene una ventaja, al reflejar los cambios habidos en los hábitos de compra, dado que pondera el indice por la cantidad consumida en el momento actual. No obstante, entre las desventajas, cabe destacar el hecho de que requiere los datos de cantidad para cada periodo de cálculo, lo que hace más laborioso su cálculo. También hay que tener en cuenta que la cesta de ponderación es inexistente en la realidad (puesto que se valora la cantidad actual a los precios del periodo base), lo que hace que sea imposible el atribuir las variaciones habidas en el índice exclusivamente a cambios en los precios. Otro efecto que tiene, el utilizar las cantidades actuales es que sobrepondera los productos cuyos precios disminuyen, puesto que se consumirá más de ellos en el periodo actual.
Para facilitar la comprensión de estos índices, vamos a desarrollar un ejemplo en el capítulo 4.1, donde se va a poder ver la construcción de estos índices para el caso de una pequeña cesta de compra compuesta por tres productos: leche, carne y fruta.

4.1. Ejemplo de números índices complejos
En la siguiente tabla, se presentan los datos para una sencilla cesta de consumo compuesta por tres productos: leche, carne y fruta, durante los años 2013, 2014 y 2015.

Se pide:
a) Obtener los índices de precios de Laspeyres, Paasche y Fisher para los tres años, de precio y cantidad, considerando 2013 como año base.
b) Obtener los índices de cantidad y valor (Laspeyres, Paasche y Fisher)
RESPUESTA
Partimos de las formulas conocidas de cada índice de precios (Laspeyres, LP, Paasche, Pp y Fisher, Fp):
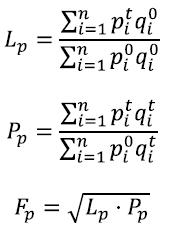
Nótese que el llamado índice ideal de Fisher es la raíz cuadrada de los dos primeros expuestos.
Aplicando las formulas a los datos del problema, proporcionados en el enunciado, nos queda para cada uno de los años, el siguiente valor de los índices:


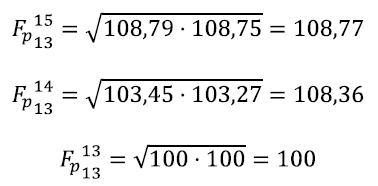
b) Vamos a calcular ahora los índices de cantidad. En este caso vamos a medir la evlolución en el periodo de la cesta de unidades físicas de leche, carne y fruta que integra nuestra cesta.
Partimos de las fórmulas para los mismos tres índices anteriores (Laspeyres, Lq, Paasche, Pq y Fisher, Fq):
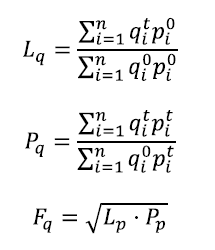
Aplicamos estas formulas a los datos proporcionados por el ejercicio, llegando a los siguientes resultados:


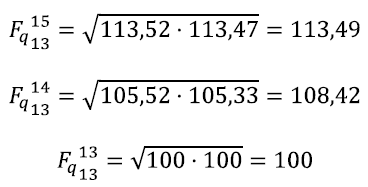
Ahora, calculamos los índices de valor, a partir de su formulación y los datos de la tabla:
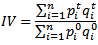
El indice valor tiene la particularidad de ser igual al producto de los índices de Laspeyres y Paasche (siendo uno de precios y otro de cantidad, es decir: Lp·Pq, o, Lq·Pp), o bien el producto de los índices de Fisher de precio y cantidad (Fp·Fq):
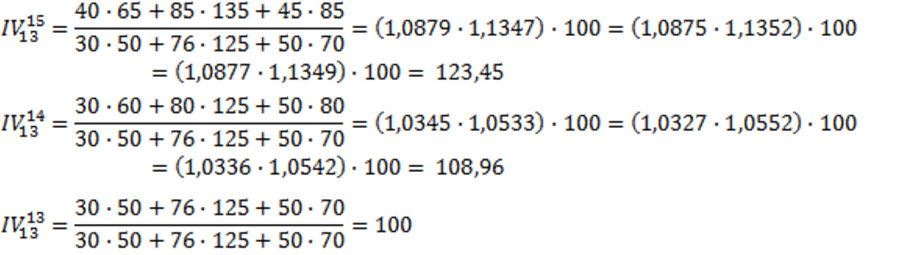
5. Tipos de índices de precios
Cuando nos circunscribimos a los índices de precios, el problema se aborda desde dos ópticas: elaborando índices con base económica, elaborando índices con base estadística.
- Índices con base económica - se basan en la existencia de relaciones entre precios y cantidades que concluyen en una relación de dependencia entre ambas. Es decir, una definición de tipo funcional. Un ejemplo de este tipo de índice es el ICV (Índice del Coste de la Vida)
- Índices con base estadística - en el segundo tipo de índices estas series de precios y cantidades pueden tratarse como colectivos distintos e independientes. La mayoría de las estadísticas oficiales publican índices de precios de este tipo, como es el caso del IPC.
5.1. Índices de base económica
Dentro de los índices con base económica se engloba, en su origen, el llamado Índice del coste de la vida. Existen diferentes definiciones que explican la concepción de un indicador de este tipo. En líneas generales, se trata de medir la variación del gasto en que tiene que incurrir el consumidor para mantener la misma satisfacción -el mismo nivel de vida- en dos momentos del tiempo, si solo difieren los precios entre ambos momentos.
El gran problema con el que nos encontramos en una definición de este tipo es la dificultad para encontrar un concepto claro de lo que es un índice del coste de la vida, ya que implícitamente es necesario definir un nivel de vida y una función de utilidad que determine la satisfacción.
Por ello, esta idea se ha ido, si no olvidando ya que siempre está abierta al debate, sí obviando a la hora de elaborar sistemas de índices de precios de consumo.
5.2. Índices de base estadística
Así como los índices funcionales de precios, o con base económica, tienen como condicionante común el que en las dos situaciones consideradas se mantuviera el nivel de satisfacción, los índices de precios con base estadística abandonan este ideal inalcanzable y se contentan con la comparación del nivel de precios en ambas situaciones.
Existen diversas fórmulas para calcular los índices de precios. Si se parte de las situaciones 0 y t, los precios Pi en ambas situaciones y las cantidades Qi que determinan la estructura de consumo dada, el índice agregativo será:
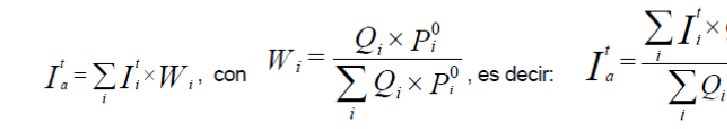
Esto nos permite definir el índice agregativo como una relación entre los costes de una determinada estructura de consumo a precios de la situación en el momentot y a precios de la situación base.
La diferente definición del conjunto {Qi} (conjunto de ponderaciones) da lugar a las numerosas fórmulas existentes en la literatura de índices.
Aunque los más utilizados son los que hemos resaltado en el punto dedicado a los índices complejos -índice de precios de Laspeyres y Paasche-, también se utilizan otros. Algunos no ponderados, como el índice de Bradstreet-Dutot o el de Sauerbeck y otros ponderados, como el índice de precios de Lowe, el de Edgeworth y, sobre todo, el denominado índice ideal de Fisher, que es igual a la raíz cuadrada del producto del índice de Laspeyres y Paasche (If = (IL·IP)1/2).
6. Utilizando números índice
Índices encadenados
Para entender el concepto de índice encadenado debemos de comprender una propiedad de este tipo de números que resulta aquí crucial. Esta propiedad es la de transitividad o circularidad, la cual podemos aplicarla al ejercicio que acabamos de realizar en la lección anterior. Por ejemplo, en el caso del índice de precios de Laspeyres, podemos descomponer el índice entre el año 2013 y 2015, como el producto entre los índices entre 2013 y 2014 por el índice entre los años 2014 y 2015: Lp1315=Lp1314·Lp1415= 108,79.
Adicionalmente, sabemos que la estructura de ponderaciones y la composición de la muestra de productos o actividades es preciso que se mantenga fija a lo largo del tiempo, lo cual va a favorecer la comparabilidad temporal. Es decir, necesitamos que durante los años en que esté en vigor la base, el índice debe medir la evolución de la variable objeto de estudio, sin que ese índice varíe, en ningún caso, por cambios en los pesos ni en la composición de la muestra.
Ahora bien, con el paso de los años, tanto la estructura de ponderaciones como el contenido de la cesta de productos o actividades que forman parte del índice van perdiendo representatividad, ya que cada vez se van alejando más del momento en que se estableció la base (por ejemplo, uno de los artículos de la cesta de la compra del IPC, base 92, cuya fórmula respondía a una base fija, era la máquina de coser, representativa a comienzos de los años 90 pero no tanto en el año 2000, cuando la base estaba llegando a su finalización).
¿Cómo resolver entonces la cuestión de la representatividad de una cesta de compra que varía con el tiempo y la necesaria comparación de los números índice calculados desde el periodo base? La respuesta es: a través del proceso de encadenamiento de índices, basado en la propiedad transitiva expuesta.
Como acabamos de decir, la mayoría de las estadísticas cambian la composición de la muestra a lo largo del tiempo, lo cual supone un problema. Cuando esto sucede, la tasa de variación mensual incorpora tanto la evolución real de la variable como la parte afectada por el cambio de muestra. Para facilitar la comparabilidad temporal, se suele calcular la variación mensual con las unidades comunes entre los dos periodos consecutivos.
Conforme va pasando el tiempo desde el año base, los índices de los componentes van cambiando según la evolución de la variable (aquellos componentes cuya variable haya aumentado más tendrán un índice mayor que otras con menores evoluciones); cuanto mayor sea el valor del índice de un componente respecto al índice general más peso relativo tendrá el componente en el momento de agregarlo para obtener el índice global.
En este tipo de índices, la estructura de ponderaciones y la composición de la muestra de productos o actividades cambian generalmente cada año. Esto favorece la representatividad, ya que el indicador se va adaptando de forma permanente a la realidad económica, pero va en perjuicio de la comparabilidad temporal, ya que la evolución estimada de la variable objeto de estudio se ve ‘contaminada’ por cambios en los pesos o contenido de la cesta de productos o actividades. Desde el punto de vista de la fórmula general de cálculo, en la práctica su construcción consiste en cambiar la referencia de la variable objeto de estudio y, consecuentemente, también las ponderaciones, cada año. Habitualmente, el periodo de referencia es o bien el mes de diciembre del año inmediatamente anterior al corriente o bien el último trimestre de dicho año.
La expresión matemática de un índice con referencia en el mes de diciembre es la siguiente:
![]()
donde:
dict-1IGmt es el índice general del mes corriente m del año t referenciado al mes de diciembre del año t-1.
dict-1Iimt es el índice del componente elemental i de la muestra (índice elemental), en el mes corriente m del año t referenciado al mes de diciembre del año t-1.
WI es la ponderación del elemento i referenciada al mes de diciembre del año t-1.
El índice elemental (índice de cada uno de los componentes elementales de la muestra) se calcula de la siguiente forma:
![]()
donde:
dict-1Iimt es el índice elemental del componente i, en el mes corriente m del año t referenciado al mes de diciembre del año t-1.
Ximt es el valor de la variable objeto de estudio del componente elemental i, en el mes corriente m del año t.
XIdict-1 es el valor de la variable objeto de estudio del componente elemental i, en diciembre del año t-1.
Como se observa en las fórmulas anteriores, los índices (elementales y agregados) están referenciados a diciembre del año anterior al corriente (t-1). Esto quiere decir que a comienzos de cada año el índice cambia de periodo de referencia, lo que conlleva discontinuidad en las series de índices. Esta es la razón por la que es necesario realizar un proceso de encadenamiento, que no es otra cosa que enlazar las series de los índices de cada año para ofrecer una serie continua en el tiempo.
Cambio de base
Cada cierto tiempo, se hace necesaria una revisión y renovación de los elementos estructurales del indicador, de su propio contenido metodológico y/o del tratamiento de la información relacionada con la propia variable objeto de estudio, los cuales intervienen en el cálculo del índice.
Esto es lo que se denomina un cambio de base.
Si bien es cierto que la revisión es necesaria en todos los aspectos que conforman el cálculo del indicador, lo que habitualmente determina el momento del cambio de base es el grado de pérdida de representatividad de los elementos utilizados en el cálculo del Sistema vigente (las actividades, en el caso de indicadores de actividad, o los productos cuando hablamos de precios) y sus ponderaciones. Por tanto, un cambio de base es una adaptación del indicador a los cambios acaecidos en la realidad económica que se pretende medir.
La periodicidad con la que se lleva a cabo un cambio de base, en teoría, depende del grado de dinamismo del sector al que se refiera el indicador. Cuanto más rápidos sean los cambios en el mismo, con mayor frecuencia deberían realizarse los cambios de base. En general, en los principales foros internacionales se ha convenido que lo idóneo es realizar un cambio de base cada cinco años (de hecho, el Reglamento del Consejo sobre estadísticas coyunturales así lo estipula).
Cuando tenemos datos de un número índice con dos bases distintas, procederemos como acabamos de hacer en el anterior ejemplo práctico.
Repercusión
La variación de un índice agregado viene determinada por el comportamiento de sus componentes. Así, cuanto mayor sea la variación del índice de un elemento, mayor será su influencia en el agregado. Pero, además, ante tasas de variación iguales entre distintos componentes, tendrá mayor influencia en el agregado aquella que lleve asignada una mayor ponderación. Esta idea intuitiva se formaliza mediante el concepto de repercusión.
La repercusión que la variación de un elemento o conjunto de elementos tiene en la variación de un índice agregado entre dos periodos m y m’, es la variación que éste hubiera experimentado si solo hubiera variado dicho elemento o conjunto de elementos. Es decir, la repercusión es la variación del índice agregado debida únicamente a la variación en uno de sus componentes. Su fórmula es la siguiente:
![]()
Donde:
RIm,m´´ es la repercusión del elemento i en el agregado.
Itm es el índice del componente i en el momento m
Itm´es el índice del componente i en el momento m’.
Wi es la ponderación del componente i en tanto por uno.
Im´es el índice del agregado en el momento m’.
Una propiedad fundamental que surge de la propia definición de la repercusión es que la suma de las repercusiones de los componentes es la tasa de variación del agregado. Esto aporta una información muy valiosa a la hora de analizar el comportamiento de cualquier índice, como complemento del estudio de las tasas de variación.
En los índices calculados siguiendo la fórmula de base fija esto es así para todos los tipos de variaciones. Sin embargo, esto no siempre es así en los índices encadenados: dado que cada año los índices deben encadenarse con coeficientes de encadenamiento diferentes, la suma de las repercusiones anuales no es igual a la tasa anual (que se obtiene utilizando índices encadenados).
Participación
Algunos autores se refieren al concepto de participación como el cociente entre la repercusión de cada índice componente y la variación total:
![]()
La interpretación de los resultados hay que hacerla con cuidado, ya que la sólo tendría sentido su utilización como porcentaje de la variación total cuando todas las variaciones de los componentes fuesen en la misma dirección (todas positivas o todas negativas).
Además, si la variación global fuese nula debido a que sus dos elementos hubiesen experimentado variaciones de +50% y de –50%, respectivamente, no tendría sentido dividir las repercusiones entre cero.