Una introducción a los números índice

Se calculan como agregaciones de índices simples. En su cálculo pueden intervenir diferentes factores de ponderación dependiendo de la naturaleza del índice. Sin embargo, el potencial real de los números índices se pone de manifiesto cuando se trata de medir varias variables o elementos en esas dos situaciones, ya que es en ese momento cuando es preciso corregir el problema que supone la agregación de variables con diferentes unidades de medida (heteromensurabilidad). Un ejemplo de su necesidad, lo vemos cuando pretendemos construir un índice de precios de una cesta de la compra donde se incluyen productos diferentes (comida, bebida, ropa, etc.), o bien, el caso de un índice bursátil compuesto  por la cotización de títulos de empresas y sectores diferentes (comunicaciones, químicas, eléctricas, bancos, etc.).

Para construir este tipo de índices, debemos de resolver dos cuestiones principales:

1. El promedio - se debe de abordar la cuestión de cómo se van a agregar los índices simples para hallar el valor final del promedio que es todo índice complejo. En este caso, podemos utilizar la media aritmética, geométrica, armónica o agregativa, con el fin de solventar este propósito. Estas medias podrán ser, a su vez como explicamos a continuación, ponderadas o no ponderadas.
2. Las ponderaciones - el indice complejo será un valor promedio de los indices que lo componen, por lo que una de las primeras cuestiones es establecer ese peso de los números índice simples dentro del valor del indice complejo final. Si la ponderación de cada índice simple es la misma, hablamos de índices complejos sin ponderar; por el contrario, cuando la ponderación de cada índice simple es distinta, hablamos de índices complejos ponderados.

A partir de aquí, trabajaremos con este tipo de índices. Podremos ver la construcción de los dos más utilizados: el índice de Laspeyres y de Paasche, exponiendo las ventajas e inconvenientes de cada uno.

Siendo:

w_i = ponderación del elemento i.

p_i^t = precio del bien i en el momento actual t.

p_i⁰ = precio del bien i en el periodo base 0.

q_i^t = cantidad (consumida, vendida o producida) del bien i en el momento actual t.

p_i⁰ = cantidad del bien i en el periodo base 0.

• Índice de Laspeyres (I_L)- es la media aritmética ponderada de los índices simples que lo integran. Como ponderación se utiliza, para cada artículo, el valor de la cantidad (consumida, vendida o producida) del bien iésimo en el período base al precio de ese mismo período base (w_i=p_i⁰·q_i⁰).

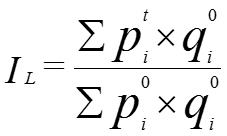
El índice de Laspeyres tiene como principal ventaja el hecho de utilizar cantidades de un solo periodo, el periodo base, por lo que las variaciones que pueda experimentar el índice serán solamente atribuibles a la variación en los precios. Entre las desventajas, destaca el hecho de que este índice pondera más los productos cuyos precios aumentan; igualmente, tampoco refleja los cambios que hayan podido haber en los patrones de compra entre el periodo base y el periodo actual.

• Índice de Paasche (I_p) - es la media aritmética ponderada de los índices simples que lo integran. Como ponderación se utiliza, para cada artículo, el valor de la cantidad (consumida, vendida o producida) del bien íesimo en el periodo actual a precio del período base (w_i=p_i⁰·q_i^t).

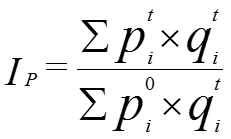
Obsérvese que el índice de Paasche tiene una ventaja, al reflejar los cambios habidos en los hábitos de compra, dado que pondera el indice por la cantidad consumida en el momento actual. No obstante, entre las desventajas, cabe destacar el hecho de que requiere los datos de cantidad para cada periodo de cálculo, lo que hace más laborioso su cálculo. También hay que tener en cuenta que la cesta de ponderación es inexistente en la realidad (puesto que se valora la cantidad actual a los precios del periodo base), lo que hace que sea imposible el atribuir las variaciones habidas en el índice exclusivamente a cambios en los precios. Otro efecto que tiene, el utilizar las cantidades actuales es que sobrepondera los productos cuyos precios disminuyen, puesto que se consumirá más de ellos en el periodo actual.

Para facilitar la comprensión de estos índices, vamos a desarrollar un ejemplo en el capítulo 4.1, donde se va a poder ver la construcción de estos índices para el caso de una pequeña cesta de compra compuesta por tres productos: leche, carne y fruta.