Una introducción a los números índice
Una introducción a los números índice
El objetivo de este libro es enseñar la teoría de números índices, en sus diversas modalidades, y en particular profundizar en el Índice de Precios al Consumo (IPC).
5. Tipos de índices de precios
5.2. Índices de base estadística
Así como los índices funcionales de precios, o con base económica, tienen como condicionante común el que en las dos situaciones consideradas se mantuviera el nivel de satisfacción, los índices de precios con base estadística abandonan este ideal inalcanzable y se contentan con la comparación del nivel de precios en ambas situaciones.
Existen diversas fórmulas para calcular los índices de precios. Si se parte de las situaciones 0 y t, los precios Pi en ambas situaciones y las cantidades Qi que determinan la estructura de consumo dada, el índice agregativo será:
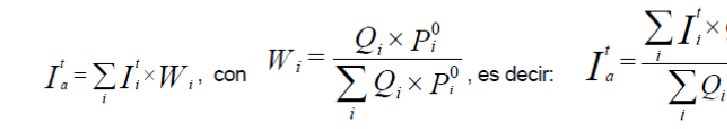
Esto nos permite definir el índice agregativo como una relación entre los costes de una determinada estructura de consumo a precios de la situación en el momentot y a precios de la situación base.
La diferente definición del conjunto {Qi} (conjunto de ponderaciones) da lugar a las numerosas fórmulas existentes en la literatura de índices.
Aunque los más utilizados son los que hemos resaltado en el punto dedicado a los índices complejos -índice de precios de Laspeyres y Paasche-, también se utilizan otros. Algunos no ponderados, como el índice de Bradstreet-Dutot o el de Sauerbeck y otros ponderados, como el índice de precios de Lowe, el de Edgeworth y, sobre todo, el denominado índice ideal de Fisher, que es igual a la raíz cuadrada del producto del índice de Laspeyres y Paasche (If = (IL·IP)1/2).